Kundenzátor

Érdekes matematikai "probléma" az, hogy vajon hányszor lehet félbehajtani egy papírlapot? Érdekesebb kérdés viszont az, hogy ha mondjuk százszor félbehajtasz egy papírlapot, az vajon milyen vastag lesz?

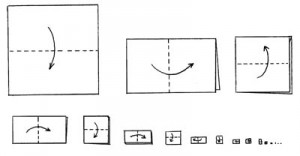
Népi bölcseletként vagy esetleg szájhagyomány útján az a mondás terjeng, hogy ötnél többször nem lehet félbehajtani a papírt. Mytbustersék ki is próbálták egy focipályányi papírlappal (meg egy kis úthengeres illetve targoncás segítséget igénybe véve), és 11-ig jutottak. A világrekord 2002 óta 12 félbehajtás, beállítója Britney Gallivan, akinek teljesítményéről külön Wikipédia oldal emlékezik meg. És hogy mi lenne, ha egy papírlapot ötvenszer félbe tudnánk hajtani? Malcolm Gladwell így ír erről Fordulópont című könyvében:

Adjunk valakinek egy nagy ív papírt és azt kérjük, hajtsa össze egyszer, aztán fogja ezt az összehajtott papírt, és még egyszer hajtsa össze, aztán még egyszer és még egyszer, egészen addig amíg ötvenszer el nem végezte a hajtás műveletét. Aztán megkérdezzük, mit gondol milyen magas lesz az összehajtogatott papír. A kérdésre a legtöbben úgy válaszolnak, hogy gondolatban összehajtják a papírt, és azt mondják, olyan vastag lenne, mint egy telefonkönyv, vagy ha elég merészek, azt mondják, olyan magas lenne, mint egy hűtőszekrény. Ám a valódi, a helyes válasz az, hogy körülbelül olyan magas lenne, mint a Föld-Nap távolság, és ha még egyszer összehajtanánk, kétszeres Föld-Nap távolságot kapnánk. Ez a példa a matematikában mértani sorozatként, avagy mértani haladványként ismeretes. … Az embernek elég nehéz ezt a fajta haladványt hétköznapi ésszel felfogni, mert az eredmény – a hatás – igen aránytalannak látszik a kiinduló ponthoz képest. A járványok hatásának felbecsülésében félre kell tennünk az arányosságnak, az ok-okozati viszonynak ezt a fogalmát. Fel kell készítenünk magunkat a lehetőségre, hogy néha kis eseményekből nagy változások lesznek, és néha ezek az események bizony nagyon gyorsan következnek be.

Aki kíváncsi rá, vagy netán ennél is többre vágyik, egy itt látható táblázatban a 100. hajtogatás hatásáig is eljut. Aztán már nincs tovább, legalábbis ebben az univerzumban. [Folding Paper in Half 12 Times] [Wikipedia: Mathematics of  paper folding]